
写在前面
这是篇为了记录计算机基础知识学习笔记的博客,希望自己能够充分利用博客这个工具,提高自己的学习效率和改善学习效果。另外,这也是在接下来的计算机二级考试的备考内容之一。这会是一篇持续更新的博客,希望能够写得完善一些。
1. 什么是算法?
算法是指对解决方案的准确而完整的描述,简单来说,就是解决问题的步骤。
| 基本特征 | 具体描述 |
|---|---|
| 可行性 | 步骤可以实现,执行能够达到预期目的 |
| 确定性 | 步骤明确,每一步意义清晰 |
| 有穷性 | 有限步骤,有限时间内能完成 |
算法的复杂度
- 时间复杂度:执行算法所需要的计算工作量
- 空间复杂度:执行算法需要的内存空间
2. 数据结构的基本概念
(1)什么是数据结构?
数据结构值得是相互有关联的数据元素的集合。
- 逻辑结构
- 存储结构
(2)数据结构的表示
1 | B = (D, R) |
| 基本概念 | 含义 |
|---|---|
| 根节点 | 数据结构中没有前件的节点 |
| 叶子节点 | 没有后件的节点 |
| 内部节点 | 除了根节点和叶子节点外的节点 |
| ### (3)线性结构与非线性结构 | |
| 基本概念 | 含义 |
| —- | —- |
| 线性结构 | 非空,每一个节点最多有一个前件和一个后件 |
| 非线性结构 | 非空,每一个节点可以有多于一个前件或后件的数据结构 |
3. 线性表及其顺序储存结构
(1)线性表
线性表即线性数据结构,表示如下
1 | (a1, a2, a3, ...,ai,...,an) |
通常,线性表可以采用顺序存储和链接存储两种存储结构
|基本概念|含义|
|—-|—-|
|顺序存储|存储地址是连续的、相邻的|
|链接存储|存储地址可以不连续,不过在逻辑上是连续的,
由头指针和尾指针进行定位|
采用顺序存储是表示线性表最为简单的方法,这种顺序表示的线性表也称顺序表
4. 栈(Stack)与队列(Queue)
(1)栈及其基本运算
栈是一种特殊的线性表,先进后出、后进先出原则,操作有三:入栈、退栈、读栈
(2)队列及其基本运算
队列也是一种特殊的线性表,先进先出、后进后出,运算多为指针头移动
循环队列:即最后一个元素的指针将指回第一个元素前一个空元素的位置,导致前后相连。
5. 线性链表
(1)线性链表的基本概念
线性链表是指在线性表的链式存储结构,简称链表。占用空间除了数据域,还有指针域,故而会比较多空间。一般链表为单向链表,但是如果在每一项之中添加一个指向前一个元素的指针,那就可以变成双向链表。
| 类型 | 优点 | 缺点 |
|---|---|---|
| 顺序表 | (1)可以随机存取表中任意节点 (2)地址顺序即逻辑顺序,无需额外空间 |
(1)插入和删除的运算效率低下 (2)储存空间不便于扩展 (3)不便于储存空间动态分配 |
| 链表 | (1)插入、删除只需移动指针,无需移动储存位置 (2)空间易扩展,方便动态分配空间 |
需要额外的空间储存逻辑关系,存储密度比顺序表低 |
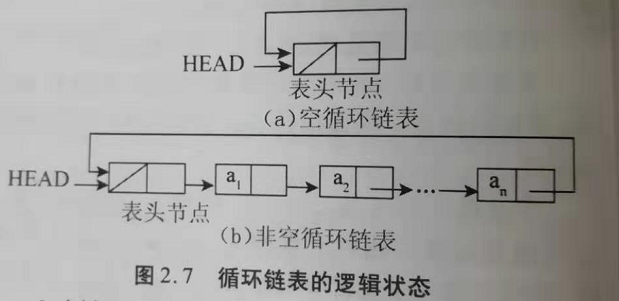
(2)循环链表
在单链表的第一个节点前增加一个表头节点,队头指针指向表头节点,最后一个节点的指针域的值由NULL改为指向表头节点,这样就形成了一个循环链表。
在循环链表中,只要知道了一个节点的位置,就可以从它出发访问到所有的节点,并且在链表为空时,链表中仍然还有表头节点这个节点,因此能够当成非空链表运算,因此统一了空链表与非空链表的运算。
6. 树与二叉树
(1)树的基本概念
树(Tree)是一种简单的非线性结构。例如家族族谱关系等。
| 基本概念 | 含义 | 例子 |
|---|---|---|
| 父节点 | 在树结构中,每一个节点只有一个前件, 即它的父节点,所有节点最终的父节点 为根节点。 |
如从一棵树的所有枝丫都发源于树干,树干有个根。 |
| 子节点 | 每个节点可以有多个后件,这些后件即为子节点,没有后件的节点称为叶子节点 | 正如树的叶子是树的结构的末端,其后没有其他节点了 |
| 度 | 一个节点拥有的后件的个数称为该节点的度,所有节点中最大的度即为该树的度(注意,后件的后件不是该节点的后件)。 | 例如树的各个枝丫上有数量不同的枝丫或者树叶,这个数量就是目前枝丫的度 |
| 深度 | 定义根所在的层次为1,其他节点所在层次等于它的父节点所在层次+1,树最大的层次即为树的深度 | 如果从根算起,最多共经过4次转折到达了叶子的节点,那么这棵树的深度即为4+1=5 |
| 子树 | 在树中,以某一个节点为根构建的新的树,称为该树的子树 | 相当于树上的大树枝,如果把大树枝看成是起点的话,那这个构建的新的树就是原来树的子树 |
(2)二叉树
二叉树与树不同,但是与树的结构很相似。(我个人觉得,二叉树就是一种特殊的树结构)
特点如下
- 可以为空,空的二叉树没有节点,非空的二叉树有且只有一个根节点。
- 每个节点最多有两棵子树,即不存在度大于2的节点。
- 子树有左右之分,次序不能颠倒。
性质如下
- 在二叉树的第k层上最多有2^(k-1)个几点,k大于等于1。
- 深度为m的二叉树,最多有2^m-1个节点(比如深度为4的树最多有2^4-1=16-1=15个节点)。
- 任何一棵树,其中度为0的叶子节点总是比度为2的节点的数量多1个(可以自己分类讨论进行验证)。
- 具有n个节点的二叉树,其深度至少为n对2取对数运算的整数部分(记为d),则深度至少为d+1,即相当于是2^d-1=n。
- 具有n个节点的完全二叉树的深度为d+1(d含义同上)。
满二叉树是指除了最后一层外,其他层的节点都是度为2的节点。完全二叉树是指除了最后一层外,每一层的节点数均达到最大值,在最后一层上只缺少右边的若干节点的二叉树。
(3)二叉树的存储结构
在计算机中,二叉树通常采用链式存储结构。其存储的节点由数据域与指针域两部分组成,由于每一个节点可以有两个后件,所以每个节点需要有2个指针,分别为左指针域和右指针域。二叉树的链式存储结构也叫二叉链表。
| 遍历方法 | 含义 |
|---|---|
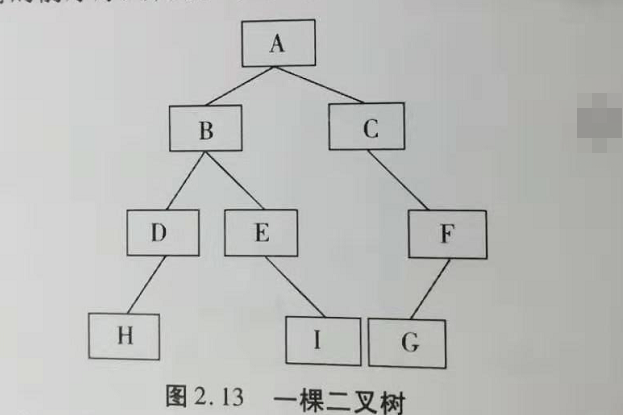
| 前序遍历 | 首先访问根节点,然后按照先左后右的原则一直访问到叶子节点,例子如下图前序遍历,遍历顺序为A B D H E I C F G。 |
| 中序遍历 | 首先遍历左子树,然后访问根节点,最后遍历右子树。例子如下图,遍历顺序为H D B E I A C G F。 |
| 后序遍历 | 先左子树,后右子树,最后根节点。如下图,遍历顺序为H D I E B G F C A。 |
7. 查找技术
| 概念 | 含义 | 分析 |
|---|---|---|
| 顺序查找 | 从线性表的第一个元素开始,逐个比较最终找出目标元素,查找停止 | (1)最好的时候,第一个即为查找元素,比较次数为1。 (2)最坏情况,最后一个才是目标元素,比较次数为n。 综上,平均为(n+1)/2 |
| 二分法查找 | 在有序的线性表中,将查找元素与中间元素进行比较,以指数级速度缩小查找范围,最终锁定目标元素。 | 最好情况为比较1次,最差情况为比较log..n次(‘..’表示数字‘2’)。 |
8. 排序技术
| 概念 | 含义 | 分析 |
|---|---|---|
| 冒泡排序法 | 通过两两相邻的数据之间比较,不断调整大小顺序,不断的重复,直到所有的数据都有序为止 | 最坏情况,比较次数为(n-1)n/2 |
| 快速排序法 | 在待排序元素中选取一个数K(一般为第一个数),以K为标准,大于K的排在K后面,小于K的排在K前面,得到两个子表,对这两个子表进行同样的操作,直到所有的数均有序后停止。 | 最坏情况,比较次数为(n-1)n/2 |
| 简单插入排序法 | 把待排序的n个元素看成是有序表和无序表,最开始有序表只有1个元素,无序表有n-1个元素,接下来在无序表中选取元素插入有序表中的正确位置,重复操作直到所有元素都插入到了正确的位置即停止。 | 最多比较(n-1)n/2次 |
| 希尔排序 | 将n个元素分为a1个组(a < n),在每一组之间进行简单排序,再将序列分为a2个组(a2 < a1),重复操作,直到最后an=1,即只有一个分组时排序完成。 | 最多次数为n^r,其中(1< r < 2)。 |
| 简单选择排序法 | 先选出最小元素与第一个元素交换位置,剩下元素再找最小元素与第二个元素交换位置,直到所有排序完毕。 | 最多比较(n-1)n/2次 |
| 堆排序法 | 堆是一个比较特别的完全二叉树的结构,在这种特殊情况下进行特殊排序,称为堆排序法。 |
最多nlog..n次,其中‘..’表示数字‘2’。 |
堆是用数组表示的二叉树,在堆里面,只有数组元素的排列顺序,没有额外的逻辑数据,在某些条件下,堆的优势很明显。
结语
写到这,关于数据结构与算法的基础入门知识就是这些了,还有一些其他内容还要进一步学习。
