
微积分的建立基石
最近在复习高数,刚刚看完了极限和导数的相关内容,有一些新的收获。回想在大一刚刚开始学习高数的时候,整个知识体系并不完整,没有办法看到全貌,实际上是一团浆糊,所以没有意识到极限之于微积分的重要性,也没有掌握到微积分的精髓。现在仔细看来,微积分之所以成为了近几百年来的数学的智慧的结晶,极大地推动了社会和科学的发展,主要得益于微积分的严谨性。正是因为微积分建立在严丝无缝的数学基石上,才能够屹立百年不倒,并且一直照耀着科学的发展。
极限
极限在数学里描述的是一种无限接近的状态,当极限值和真值之间的差值足够小(小于任意给定正数)的时候,我们认为,这就是真值,这时极限值即为极限。正是因为小于任意给定的正数这个定义,让极限变得牢不可破,这才使得它可以支撑起微积分的整个大厦。
连续、可导、可微、可积、等价无穷小、邻域、去心邻域等等基本概念都是建立在极限的基础上的,这一点可以从这些概念的原始数学定义中得证。没有极限就没有这些概念,没有这些概念也就没有微积分,又或者是如果极限本身的数学定义有漏洞,也支撑不起微积分几百年的发展。
各种概念
极限
在函数中,对于任意给定的
$a>0$,存在$X>0$,当$|x|>X$时,就有$|f(x)-A|<a$,此时,$f(x)$就收敛于$A$,或者说$A$是函数$f(x)$的极限。符号记为:$\lim_{x\to\infty}{f(x)}=A$
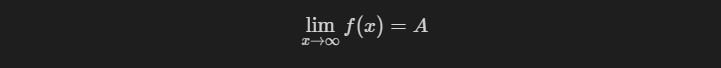
邻域
设
$\delta>0$,实数集$U_\delta(x_0)={\{x||x-x_0|<\delta\}}$称为$x_0$的$\delta$邻域。在不必说明邻域半径$\delta$大小时,简记为$U(x_0)$,称为$x_0$的某邻域。
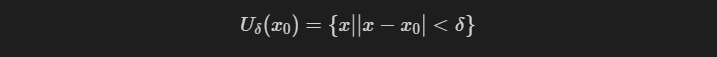
连续
如果
$f(x)$在$x=x_0$处的左极限和右极限存在且相等,则称$f(x)$在$x=x_0$处连续。即$\lim_{x\to x_0}f(x)=f(x_0)$成立时,或者即$\lim_{x\to {x_0}^{-}}f(x)=\lim_{x\to {x_0}^{+}}f(x)=f(x_0)$成立时,称$f(x)$在$x=x_0$` 处连续。
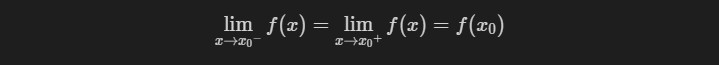
可导
设
$f(x)$在$x=x_0$的某邻域$U(x_0)$内有定义,并设$x_0+\Delta{x} \in U(x_0)$。如果
$$\lim_{x\to 0} \frac{f(x_0+\Delta{x})-f(x_0)}{\Delta{x}}$$
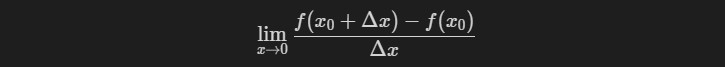
存在,则称$f(x)$在$x=x_0$处可导,并称上述极限为$f(x)$在$x=x_0$处的导数,记为
$$\lim_{x\to 0} \frac{f(x_0+\Delta{x})-f(x_0)}{\Delta{x}}=f^{'}(x_0)=\frac{df(x)}{\Delta{x}}|_{x=x_0}$$
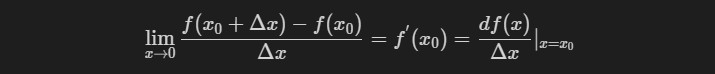
可微
设
$y=f(x)$在$x=x_0$的某邻域$U(x_0)$内有定义,并设$x_0+\Delta{x} \in U(x_0)$,如果
$$\Delta{y}=f(x_0+\Delta{x})-f(x_0)=^{can\ be\ write}=A\Delta{x}+o(\Delta{x})$$
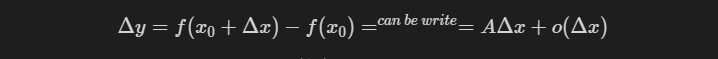
其中$A$与$\Delta{x}$无关,且$\lim_{\Delta{x}\to 0} \frac{o(\Delta{x})}{\Delta{x}}=0$,则称$f(x)$在$x=x_0$处可微。记为$dy=A\Delta{x}=Adx$
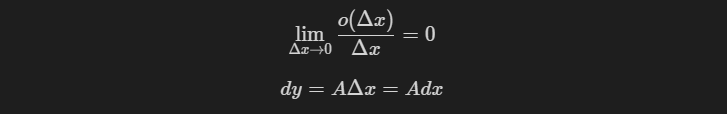
可积
设
$f(x)$在$[a,b]$上有定义且有界,如果$\lim_{\lambda\to0}\sum_i^nf(\xi_i)\Delta{x_i}$存在,则称$f(x)$在$[a,b]$上可积,并称上述极限为$f(x)$在$[a,b]$上的定积分。记为:
$$\lim_{\lambda\to0}\sum_i^nf(\xi_i)\Delta{x_i}=\int_{a}^{b}f(x)dx$$
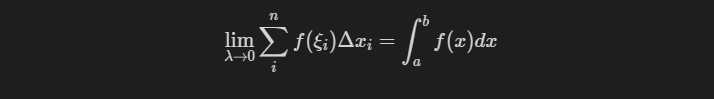
结语
根据上面列举的各种定义的数学表达式,我们能够很清晰的看出来,这些概念都是基于极限这个概念建立起来的,所以极限对于微积分的重要性不言而喻。同时,我们也应该能够明白,求解极限是微积分当中的基本运算,熟练掌握各种极限表达式的求解是后面学习导数、微分和积分的基础,所以在这里一定要打好基础,多进行练习。