
前言
常见的相关系数有三种:pearson、spearman、kendall。皮尔森(pearson)相关系数、斯皮尔曼(spearman)相关系数和肯德尔(kendall)相关系数并称为统计学三大相关系数。其中,spearman和kendall属于等级相关系数亦称为“秩相关系数”,是反映等级相关程度的统计分析指标。pearson是用来反应俩变量之间相似程度的统计量,在机器学习中可以用来计算特征与类别间的相似度,即可判断所提取到的特征和类别是正相关、负相关还是没有相关程度。
三种相关系数各有特点,但是相同的是,三种相关系数都是计算变量之间的相关性,接下来我们一一介绍:
1. pearson相关系数
pearson相关系数衡量的是线性相关关系 ,是最常用的一种相关系数,记为r。若r=0,只能说x与y之间无线性相关关系,不能说无相关关系。相关系数的绝对值越大,相关性越强:相关系数越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱。
定义: 两个变量X、Y之间的协方差和两者标准差乘积的比值
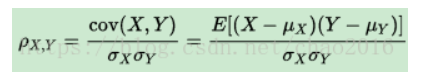
代入样本的协方差和标准差可得计算公式:
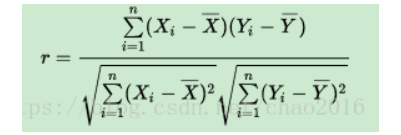
公式推导过程:
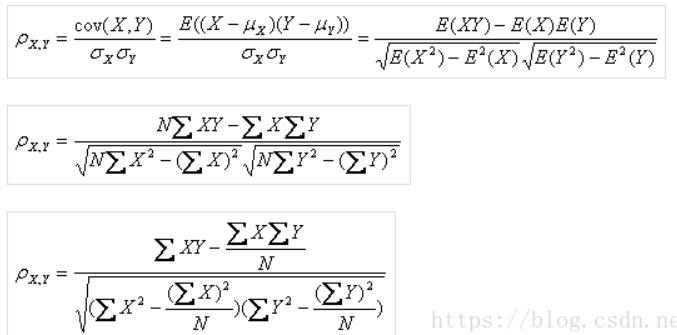
2. spearman相关系数
斯皮尔曼相关性系数,通常也叫斯皮尔曼秩相关系数。“秩”,可以理解成就是一种顺序或者排序,那么它就是根据原始数据的排序位置进行求解,这种表征形式就没有了求皮尔森相关性系数时那些限制。
计算公式:
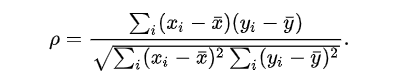
斯皮尔曼相关系数表明X(独立变量)和Y(依赖变量)的相关方向。如果当X增加时,Y趋向于增加,斯皮尔曼相关系数则为正。如果当X增加时,Y趋向于减少,斯皮尔曼相关系数则为负。斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。当X和Y越来越接近完全的单调相关时,斯皮尔曼相关系数会在绝对值上增加。当X和Y完全单调相关时,斯皮尔曼相关系数的绝对值为1。
斯皮尔曼相关系数经常被称作”非参数”的。这里有两层含义。首先,当X和Y的关系是由任意单调函数描述的,则它们是完全皮尔逊相关的。与此相应的,皮尔逊相关系数只能给出由线性方程描述的X和Y的相关性。其次,斯皮尔曼不需要先验知识(也就是说,知道其参数)便可以准确获取XandY的采样概率分布。
一般地,斯皮尔曼相关系数在有三个或更多条件的情况下是有用的。并且,它预测观测数据有一个特定的顺序。 例如,在同一任务中,一系列的个体会被尝试多次,并预测在多次尝试过程中,性能会得到提升。在这种情况下,对条件间趋势的显著性检验由E. B. Page发展了,并通常称为给定序列下的Page趋势测验。
3. kendall相关系数
肯德尔相关性系数,又称肯德尔秩相关系数,它也是一种秩相关系数,不过它所计算的对象是分类变量。
分类变量可以理解成有类别的变量,可以分为
无序的,比如性别(男、女)、血型(A、B、O、AB);
有序的,比如肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)。
通常需要求相关性系数的都是有序分类变量。

n个同类的统计对象按特定属性排序,其他属性通常是乱序的。同序对(concordant pairs)和异序对(discordant pairs)之差与总对数(n*(n-1)/2)的比值定义为Kendall(肯德尔)系数。
肯德尔相关系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验,它使用计算而得的相关系数去检验两个随机变量的统计依赖性。肯德尔相关系数的取值范围在-1到1之间,当τ为1时,表示两个随机变量拥有一致的等级相关性;当τ为-1时,表示两个随机变量拥有完全相反的等级相关性;当τ为0时,表示两个随机变量是相互独立的。
4. 结语
三种相关性系数的使用场景不尽相同,因此我们可以根据实际的使用场景来选择使用哪一种相关系数。
This is test for a new vscode widget, which named Markdown Preview Enhance, it can substitute the old preview widget inside the vscode. It provides a white background of the editor, which is more closely to the real appearance of the render html page.